April 20, 2017
Evolution of Cooperation through Longer Memory
In some dilemmas, longer memory gives rise to cooperation | IST Austria scientists develop new approach to overcome computational hurdles in analyzing cooperative strategies
When we make a decision about whether or not to cooperate with someone, we usually base our decision on past experiences—how has this person behaved in the past?—and on future reciprocity—will they return the favor?—and weigh these against the possible benefits of defecting. However, when analyzing strategies for repeated dilemmas, modeling long-term memory in cooperative strategies quickly becomes computationally intractable, and in the past, researchers have either restricted the possible strategy types, or only allowed players to make their decisions based on the previous round (“memory-1”).
One basic but important example of a social situation is the prisoner’s dilemma. In this situation, two prisoners are given the same options: remain silent or snitch on the other. If they both remain silent, they each get one year in jail. If one talks, and the other remains silent, the one who talks goes free, and the other gets three years in jail. If they both talk, they both get two years. For repeated versions of this game, a variety of successful memory-1 strategies have been found, including “Win-Stay Lose-Shift” (WSLS), where prisoners continue to cooperate or defect until this strategy gives the less desirable outcome. However, if players can remember the last two rounds (memory-2), there are 65’536 possible strategies, and if they can remember up to three rounds (memory-3), this increases to 1.84∙1019—this is already computationally infeasible, not to mention other kinds of social situations with more than two players.
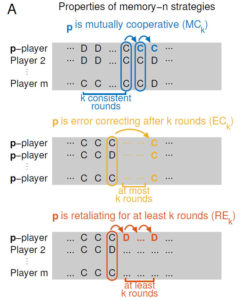
To overcome this computational challenge, IST Austria scientists and their collaborators have proposed an alternative approach to the problem of simulating these dilemmas: they have distilled a set of axioms that every robust cooperative strategy should have, and characterize the strategies that satisfy these conditions. In this way, they reduce the computation necessary for an open-ended search of all possible strategies. In particular, their axioms state that a successful cooperative strategy should be: (1) mutually cooperative, (2) able to correct errors, and (3) sufficiently retaliatory against defectors (in Figure A, MCk, ECk, and REk correspond to properties (1), (2), and (3), respectively. “C” indicates cooperation, “D” indicates defection.). The first condition corresponds to continuing to cooperate after rounds of mutual cooperation. The second means that even if a player makes a mistake, after a certain number of rounds, the players return to mutual cooperation. The last protects the group from players who might take advantage of altruism, or who might make the group too altruistic, and thus vulnerable.
They found that players with these strategies and memories of length k (that is, they remember the past k rounds of play) will only cooperate if all players took the same actions for the last k rounds (i.e. if they all cooperated or if they all defected)—giving rise to the name all-or-none (AONk) strategies. The WSLS strategy, in particular, is AON1. They moreover show that these strategies evolve naturally in a variety of different social dilemmas, and for groups of arbitrary size. Of course, not every cooperative strategy needs to be AONk to be stable. However, the authors have numerical results that indicate that all-or-none strategies (or delayed versions thereof) in fact make up all memory-2 strategies for the prisoner’s dilemma. They also make several predictions: First, if cooperation evolves in the context of a social dilemma, it is the result of all-or-none-type strategies. Second, cooperation evolves more readily in memory-2 strategies than in memory-1 strategies, under reasonable conditions. In other words, a longer-term memory increases the chance that cooperation will evolve. The group further examined the implications of players remembering only how often other players cooperated (and not when). In this case, longer memory did not lead to a greater degree of cooperation, thus indicating that successful strategies depend not only on the degree of past cooperation, but also its context.
Krishnendu Chatterjee joined IST Austria in 2009, and became full professor in 2014. He and his group are broadly interested in game theory and computer-aided verification, and one specialty of the group is evolutionary game theory. Post-doc Christian Hilbe is particularly interested in the applications of evolutionary game theory in economics and biology: “It’s fascinating to see how mathematics can be used to describe human and animal behavior in a wide range of different situations.”



