Decades-Old Erdős Conjecture Cracked

Some of the most famous problems in mathematics remain unsolved for centuries. For Erdős’ conjecture, it took fifty years for a solution to be found. Professor Matthew Kwan from the Institute of Science and Technology Austria (ISTA) and mathematicians from Harvard and MIT present a proof that shows the existence of so-called high-girth Steiner triple systems.

When Matthew Kwan heard about the Erdős conjecture during his studies, he did not expect to be part of proving this infamous mathematical theorem. In a new paper, Kwan and colleagues prove the existence of Steiner triple systems with arbitrarily high girth. For the sophisticated proof, the new ISTA faculty member Kwan collaborated with colleague Michael Simkin from Harvard University and two prodigy graduate students Ashwin Sah and Mehtaab Sawhney from the Massachusetts Institute of Technology (MIT).

Steiner triple systems are fundamental types of combinatorial designs, which have their roots in the design of scientific experiments. For example, it is important to know which grain types can flourish in various soils with different properties. How to probe all these combinations efficiently? You can in fact reduce the number of experiments with clever combinatorics. Nowadays, researchers in combinatorial design theory study more abstract settings than agriculture. Their results are relevant to computer programming and coding theory. Yet, even fundamental problems have remained unsolved. This included Erdős’ conjecture – until now.

The meaning of Erdős’ conjecture

The conjecture is concerned with so-called Steiner triple systems. Assume seven people want to form triples. Each person can be part of multiple triples, yet each pair of persons can only be part of exactly one triple. What does that mean? One individual A can be part of three triples then, forming the first triple with B and C, the second one with E and F, and the third one with D and G. At the same time, everyone else searches for partners. B for instance would not be allowed to join any triples that contain A or C because they already met them in the initial ABC triple. However, B can form two other triples still. In fact, with seven people – or points, as they are called in designs –, exactly seven triples are possible, making it a Steiner triple system.

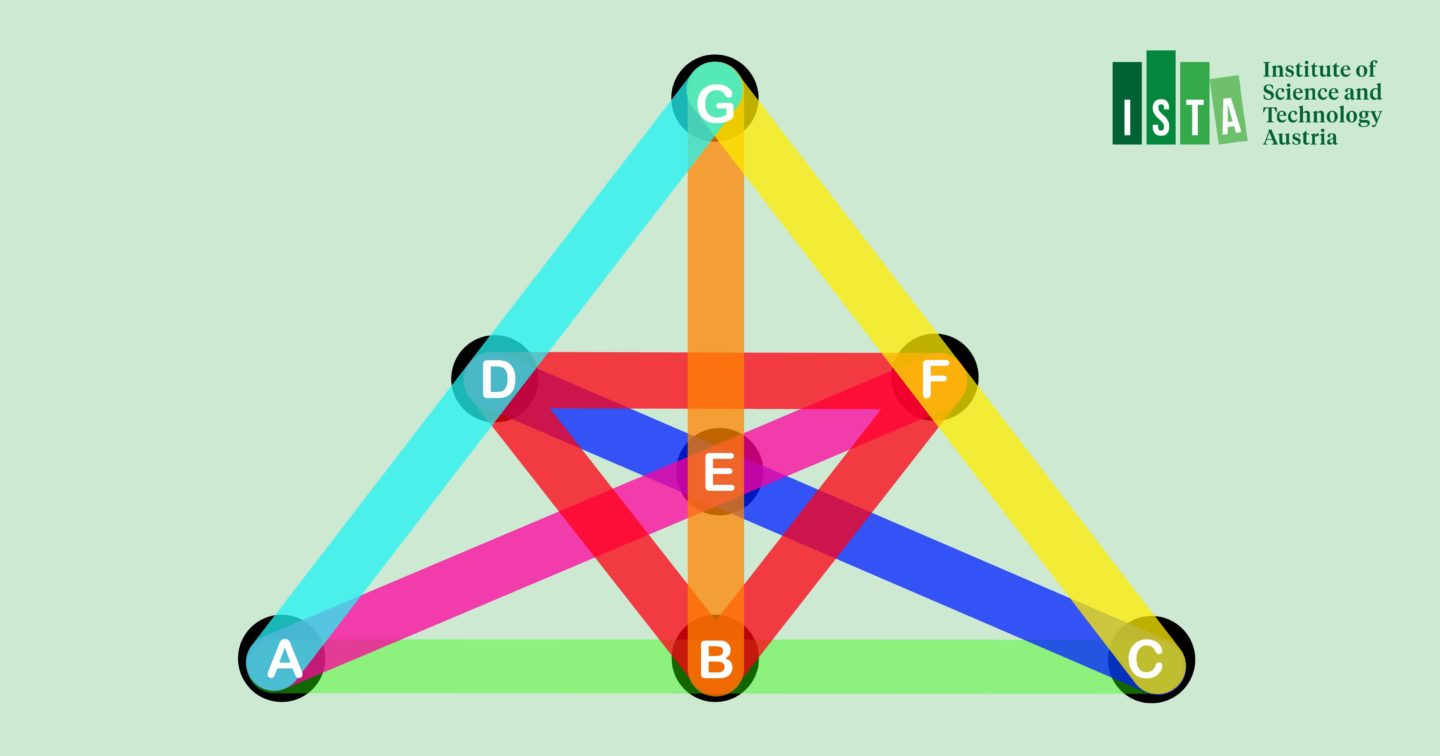
The mathematicians showed that Steiner triple systems with the desirable property of high girth indeed exist. High girth is a statistical condition. When many triples span over a small number of points the girth is low. “Many triples across few points, such dense spots inevitably appear with algebraic designs,” explains Kwan. “Erdős wondered whether you could avoid them. Where triples have no such configurations, the system is said to possess high girth. To prove their existence, you must avoid algebra and bring in probabilistic methods. That´s what we managed to do.”

Interdisciplinarity inside mathematics

In design theory, perhaps oldest field of combinatorics, there has been limited progress on fundamental questions until eight years ago. Related to Kwan’s background of probabilistic combinatorics, several probabilistic results revolutionized the field since game-changing advances in 2014. The sophisticated new proof comprises a wide array of techniques at the frontier of extremal and probabilistic combinatorics. “Additionally, we used two novel methods: Retrospective analysis, which allows us to keep track of the randomness in previous steps, and sparsification, which deals with all the obstacles that relate to that,” summarizes Kwan the technical aspects of the result.

With his group at ISTA, Kwan seeks to get a better fundamental understanding of designs, especially from a viewpoint of probability. “My philosophy of mathematics: I try to work on different things. It may be tempting to really focus on just one subfield, but when you work on various problems throughout your life, you discover techniques that help you succeed in other areas.”

Publication:      

Kwan M, Sah A, Sawhney M and Simkin M. 2022. High-girth Steiner triple systems. Preprint. arxiv.org/abs/2201.04554

Further Reading:

Erica Klarreich (2015): A Design Dilemma Solved, Minus Designs. Quanta Magazine. – A popular account of Steiner triple systems and recent breakthroughs in design theory.

Yufei, Zhao (2022): Kwan-Sah-Sawhney-Simkin: High-girth Steiner triple systems. – Detailed blog entry.