How to Turn Drumbeats Into a Math Proof

Drumbeats. Billiards on a round table. They might not appear to have much in common, but Professor Vadim Kaloshin at the Institute of Science and Technology Austria (ISTA) uses these ideas interchangeably to explore an array of intriguing questions. Now, he has received a best paper award in recognition of his work in this area. But how does beating a drum help prove a hundred-year-old conjecture about billiards? And how does mathematics reveal the deep connections between these seemingly disparate notions?

Mathematics is able to capture and describe the essential properties and underlying principles of physical systems. About a hundred years ago, G. D. Birkhoff used mathematics’ ability to abstract physical systems to turn the game of billiards into a mathematical playground. By considering the table simply as a boundary and the ball as a point mass—each endowed with a few key properties—he was able to focus on qualitative questions (e.g. about the movement of the balls or the shape of the table) without being overwhelmed by physical details.

Arguably the deepest question about mathematical billiards, the Birkhoff conjecture, is almost a century old and still unresolved. Simply put, it states that if the movement of the ball is always periodic (the ball repeats the same path) or almost periodic (the path is repeated to within a degree of accuracy), then the boundary of the table must be an ellipse (a regular oval shape). In the image below, you can see examples of periodic paths (for instance, the green and blue lines).

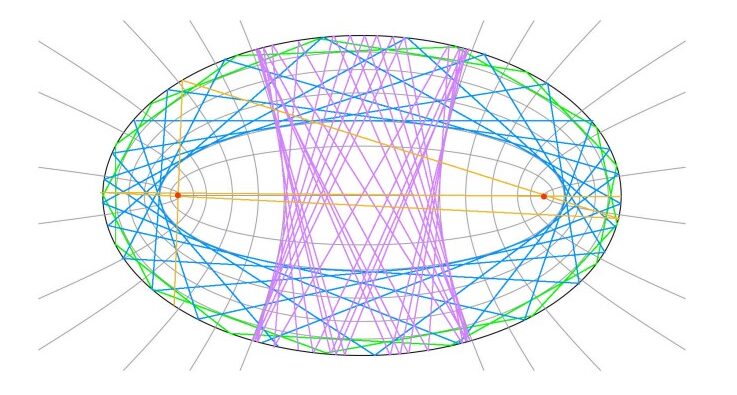
Of course, this mathematical playground quickly became more than that: with the essentials revealed, it becomes apparent that billiard-type dynamics are everywhere—the atoms of a gas moving in a container, for instance, or sound waves moving through a room. It was the latter that first caught ISTA Professor Vadim Kaloshin’s attention in the form of another question, this one over a century old.

“Can one hear the shape of a drum?”

Essentially, this question asks if the sound of a drum uniquely defines its shape. Mark Kac asked this in a paper of the same name in 1966, though similar questions have been around since the late 1800s. “I first heard about this question in graduate school,” recalls Kaloshin. “There, I focused on dynamical systems. Essentially, given an evolving system, I try to use math to explain the things that are mysterious.” Examples of such mysterious, evolving systems abound, from instability in the Kirkwood gaps in our solar system’s asteroid belt and Arnold diffusion—where Kaloshin made some of his most famous contributions—to the frequencies of differently shaped drums.

Kac’s specific question was answered in the negative in 1992, when two different shapes with the same “sound” were found:

However, many related questions remain unanswered, and Kaloshin and his group at ISTA investigate, for instance, how deformations of a drum deform its sound. “One of the techniques we use is to look at billiard paths of the sound waves,” says Kaloshin. “So we explored how we could use the sounds of drums to say something about billiard paths—that is, how could we use an application to prove something about the theory?” Thus, with beats on the brain, Kaloshin and his collaborator set about “drumming up” a proof of Birkhoff’s conjecture.

Using an application on the (dynamical system) theory

“If it sounds like an ellipse, it IS an ellipse,” is how Kaloshin describes their proof. In the end, Kaloshin and his collaborator were unable to resolve Birkhoff’s conjecture completely. However, they were able to make significant progress. Essentially, they showed that if an ellipse is deformed in a small, smooth, strictly ordered way, it will still be an ellipse. If this had not been the case, it would have disproved the Birkhoff conjecture. The resulting paper, which was published in the Annals of Mathematics, will be honored with a best paper award at this week’s International Congress of Basic Science in Beijing.

Keeping the ball rolling

In the summer of 2021, a new mind entered the picture: Illya Koval joined the Kaloshin group through the Institute’s ISTernship program. Intrigued by Kaloshin’s lectures on the topic and description of the problem, Koval set to work pushing the theory further. After several weeks, he generalized Kaloshin’s results by decreasing the restrictions on the trajectories of the billiard balls. Koval, who has since been accepted to ISTA’s PhD program and joined the Kaloshin group, is still fascinated: “The dream is to prove the global Birkhoff conjecture, but we need a new approach,” says Koval. So for now, the problem waits for Kaloshin and his team to “beat” their heads against it.

Publications: 

Kaloshin, V. & Sorrentino, A. 2018. On the local Birkhoff conjecture for convex billiards. Annals of Mathematics. DOI: 10.4007/annals.2018.188.1.6 (also available at DOI: 10.48550/arXiv.1612.09194)

Koval, I. 2023. Local strong Birkhoff conjecture and local spectral rigidity of almost every ellipse. arXiv Preprint. DOI: 10.48550/arXiv.2111.12171