August 4, 2021
Designing with Elastic Structures
New algorithm from IST Austria researchers computes stable curved beams for simple manufacturing

Curved elements are an intriguing feature of architecture yet getting the shape right has been not only a practical but a theoretical challenge. A new method developed by computer scientist Christian Hafner and his doctoral supervisor Bernd Bickel from the Institute of Science and Technology (IST) Austria is changing this. It efficiently designs flat beams that can be bent into desired shapes. In actual physical models the results are stable, and the research is now being presented at the SIGGRAPH conference.
Computer simulation is often a compromise. The more accurate it becomes, the longer the computation takes, or it requires more expensive hardware. But PhD student Christian Hafner and his supervisor Bernd Bickel from the Institute of Science and Technology Austria (IST Austria) overcame this limitation by finding a simple and exact solution for a problem in structural design.
Their clever and powerful algorithm enables the creation of curved components for architecture, which can be physically realized by bending flat beams into the desired shapes. At the prestigious SIGGRAPH conference, they introduce the results to the visual computing community.
Watch the corresponding video on YouTube
Manufactured models of the theoretical results. © IST Austria
The Physical Limits of Elastic Elements
Bending slender beams allows for the realization of spectacular structures in architecture, furniture, and product design. “But what are the physical limits for bending flat components that are fixed at both ends? What shapes are even feasible?”, Hafner wondered in the beginning of the project. “The paper answers these questions.” The program evaluates whether a desired curve is physically viable and how it can be achieved by varying the width of the beam.
Putting his mathematical and physical knowledge into practice, Hafner proved that shapes are only feasible if the curve’s inflections points lie on one straight line. “I played around for quite a long time until I realized that the equation yields a simple geometric characterization,” he shares his delight about the elegance of the theorem. “It was luck, actually, that the problem has such a simple solution.”

Manufacturing Physical Models
Another feature is the program’s ability to stabilize an unstable design by slightly adapting its shape. The design remains steady, where previously it would have buckled into a different configuration. What is more, the authors show how to optimize the beam shapes for simple manufacturing and how to balance out the effect of gravity. “When we scale to architectural applications, the impact of its dead load is very important. We also found a way to include the gravitational effect exactly without slowing down the algorithm.”
Watch the corresponding video on YouTube
Shapes that would usually buckle into another configuration can be slightly adapted in their width to remain stable. © IST Austria
Using 3D prints and cardboard models, the scientists physically built the digital results and experimentally confirmed them to be stable. While for cardboard it is rather negligible, manufacturing beams in a flat state first minimizes material waste and makes the most out of naturally elastic materials such as timber. To facilitate a diverse range of designs, the necessary stiffness can be attained in three ways: Changing the width (as previously described), perforating it, or composing two materials on top of each other.
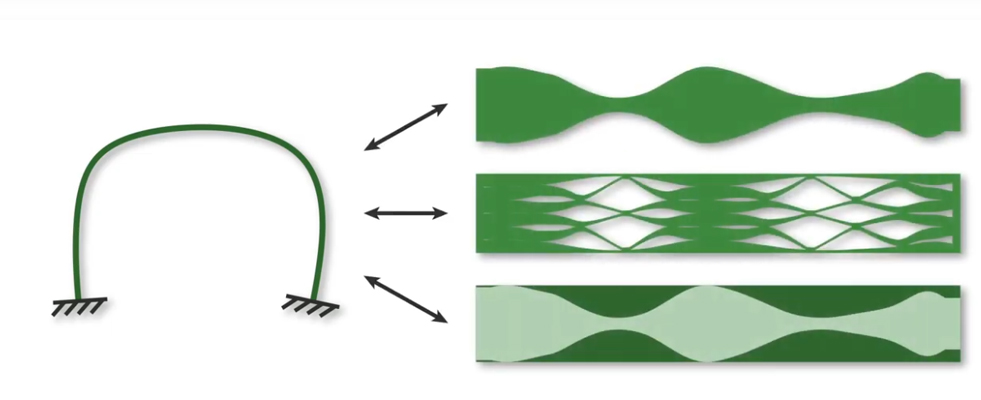
“Although I come from computer graphics, the motivation behind my research is to understand the mathematics,” Hafner expresses his fascination. In the future, he wants to extend this work to three dimensions, so beams can bend and twist in different directions, opening intriguing new avenues for structural design.
Publication
Christian Hafner, and Bernd Bickel. 2021. Design Space of Plane Elastic Curves. ACM Transactions on Graphics 40(4) (SIGGRAPH 2021). DOI: 10.1145/3450626.3459800
Funding information
The project was supported by funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement No 715767).



