Elastische Strukturen entwerfen

Gebogene Bauteile sind faszinierende architektonische Merkmale, doch die richtige Form zu finden, war bisher nicht nur eine praktische, sondern auch eine theoretische Herausforderung. Eine neue Methode des Computerwissenschafters Christian Hafner und seines Doktorvaters Bernd Bickel vom Institute of Science and Technology (IST) Austria ändert das. Sie entwirft auf effiziente Weise flache Balken, die in die gewünschte Form gebogen werden können. Die Ergebnisse wurden mit tatsächlichen physikalischen Modellen bestätigt und werden auf der SIGGRAPH-Konferenz vorgestellt.

Computersimulationen sind oft Kompromisse. Je genauer sie werden, desto länger dauern die Berechnungen, oder sie erfordern teurere Hardware. Doch der Doktorand Christian Hafner und sein Betreuer Bernd Bickel vom Institute of Science and Technology Austria (IST Austria) umgingen diese Probleme, indem sie eine einfache und exakte Lösung für ein Problem im Strukturdesign fanden.

Ihr leistungsfähiger Algorithmus ermöglicht die Herstellung gekrümmter Bauteile. Durch Biegung von flachen Balken können die gewünschten Formen physikalisch realisiert werden. Auf der renommierten Visual Computing-Konferenz SIGGRAPH stellen sie ihre Ergebnisse vor.

Zugehöriges Video auf YouTube ansehen

Gefertigte Modelle der theoretischen Ergebnisse. © IST Austria

Die physikalischen Grenzen elastischer Elemente

Das Biegen dünner Balken ermöglicht die Konstruktion spektakulärer Strukturen in Architektur, Möbel- und Produktdesign. „Doch wo liegen die physikalischen Grenzen für das Krümmen von flachen Bauteilen, die an beiden Enden fixiert sind? Welche Formen sind überhaupt machbar?“, fragte sich Hafner zu Beginn des Projekts. „Die Publikation gibt Antworten auf diese Fragen.“ Es wird untersucht, ob eine gewünschte Biegung physikalisch machbar ist und wie sie durch Variation der Breite des Trägers erreicht werden kann.

Indem er sein mathematisches und physikalisches Wissen anwendete, wies Hafner nach, dass Formen nur möglich sind, wenn die Wendepunkte der Kurve auf einer Geraden liegen. „Ich habe ziemlich lange herumgespielt, bis mir klar wurde, dass die Gleichung eine einfache geometrische Charakterisierung zulässt“, freut er sich über die Eleganz des Beweises. „Es war eigentlich Glück, dass das Problem eine so einfache Lösung hat.“

Die Herstellung physischer Modelle

Ein weiteres Merkmal ist die Fähigkeit des Programms, einen instabilen Entwurf zu stabilisieren, indem es seine Form leicht anpasst. Der Entwurf bleibt stabil, wo er vorher in eine andere Konfiguration geknickt wäre. Darüber hinaus zeigen die Autoren, wie die Balkenformen für eine einfache Herstellung optimiert werden können und wie die Wirkung der Schwerkraft ausgeglichen werden kann. „Wenn wir auf architektonische Anwendungen skalieren, ist der Einfluss der Eigenlast sehr wichtig. Wir haben auch einen Weg gefunden, die Gravitation exakt zu berücksichtigen, ohne den Algorithmus zu verlangsamen.“

Zugehöriges Video auf YouTube ansehen

Formen, die sich normalerweise in eine andere Form wölben würden, können in ihrer Breite leicht angepasst werden, um stabil zu bleiben. © IST Austria

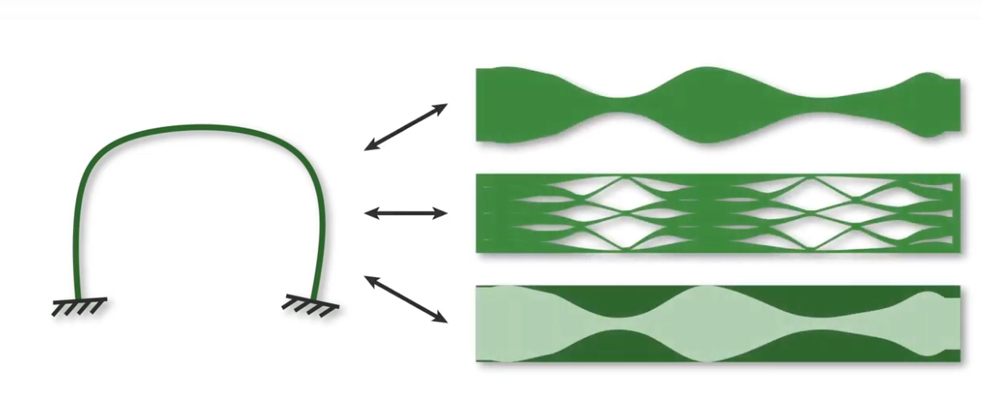
Mit Hilfe von 3D-Drucken und Karton bauten die Wissenschaftler die digitalen Ergebnisse physisch nach und bestätigten experimentell deren Stabilität. Während es bei Karton vernachlässigbar ist, minimiert die Herstellung von flachen Balken von vornherein den Materialabfall und schöpft die natürliche Elastizität von Materialien wie Holz optimal aus. Um vielfältige Konstruktionen zu ermöglichen, kann die notwendige Festigkeit auf drei Arten erreicht werden: Durch Veränderung der Breite (wie zuvor beschrieben), durch Perforation oder durch das Übereinanderlegen von zwei Materialien.

„Obwohl ich aus der Computergrafik komme, ist die Motivation hinter meiner Forschung, die Mathematik zu verstehen“, drückt Hafner seine Begeisterung aus. In Zukunft möchte er seine Arbeit auf drei Dimensionen ausdehnen, wo sich Balken in verschiedene Richtungen biegen und verdrehen können, wodurch weitere faszinierende Gestaltungsmöglichkeiten entstehen.

Publikation

Christian Hafner, and Bernd Bickel. 2021. Design Space of Plane Elastic Curves. ACM Transactions on Graphics 40(4) (SIGGRAPH 2021). DOI: 10.1145/3450626.3459800

Projektförderung

Das Projekt wurde vom Europäischen Forschungsrat (ERC) im Rahmen des Horizon 2020 Forschungs- und Innovationsprogramms der Europäischen Union gefördert (Grant Agreement No 715767).