Die Mathematik hinter Schneeflocken

Im Winter fällt Inspiration, einige der grundlegendsten Aspekte der Welt zu untersuchen, direkt vom Himmel: Schneeflocken. Ihre Symmetrie führt zur Mathematik der sogenannten Gruppentheorie, die Wissenschafter:innen auf der ganzen Welt und auch am Institute of Science and Technology (IST) Austria hilft, neue Entdeckungen in der Mathematik, Physik und vielen anderen Bereichen zu machen.

Schneeflocken sind nicht nur schön anzusehen, sie können uns auch etwas über die unserer Welt zugrundeliegenden mathematischen Strukturen lehren, nämlich über Gruppentheorie. Dieses Feld ist in vielen Bereichen der abstrakten und angewandten Mathematik von grundlegender Bedeutung und führt sogar zu wichtigen Erkenntnissen in der Grundlagenphysik, der Chemie oder der Computerwissenschaft.

Am Institute of Science and Technology (IST) Austria arbeiten mehrere Forscher:innen mit Gruppentheorie, um offene Fragen der Mathematik zu untersuchen. Einer von ihnen ist Adam Brown, ein Postdoc in der Edelsbrunner Gruppe. Er ist fasziniert von der Möglichkeit, unterschiedliche Bereiche der Wissenschaft durch Symmetrie zu verbinden: „Symmetrie hilft uns, versteckte Verbindungen zwischen sehr unterschiedlichen Themen aufzudecken. Einige der aufregendsten Errungenschaften in der Mathematik kombinieren Techniken aus verschiedenen Disziplinen, wie etwa der Zahlentheorie und der Geometrie, indem sie deren gemeinsame Muster und Symmetrien aufzeigen.“

Spielen im Schnee

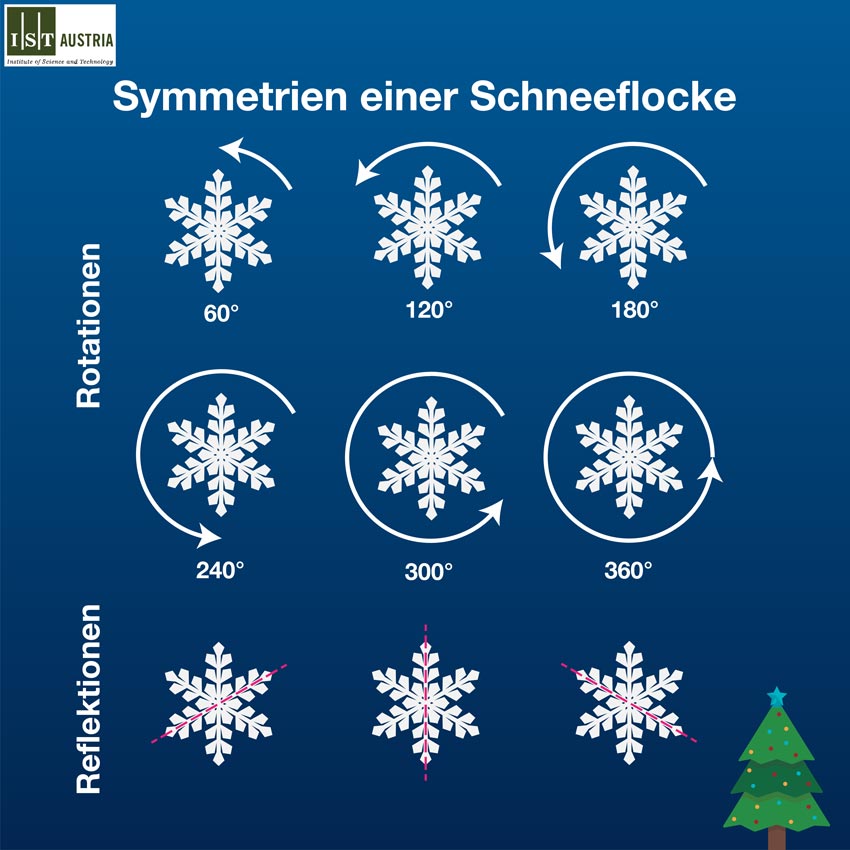
Aber was hat das mit Schneeflocken zu tun? Eine typische Schneeflocke hat eine schöne sechsseitige Symmetrie, und die führt einen zur Gruppentheorie. Eine Symmetrie in der Mathematik bedeutet einfach, dass etwas sein Aussehen und seine Eigenschaften nach bestimmten Transformationen nicht verändert. Wie in der obigen Abbildung dargestellt, sieht eine zugegebenermaßen idealisierte Schneeflocke nach bestimmten Drehungen oder Spiegelungen um bestimmte Achsen genauso aus, wie vorher. Das Wichtige dabei ist, dass das Anwenden zweier solcher Transformationen dasselbe Ergebnis liefert, wie nur eine andere Transformation. Das kann man anhand der Beispiele in der Abbildung unten sehen. Dies ist das Geheimnis der Gruppentheorie.

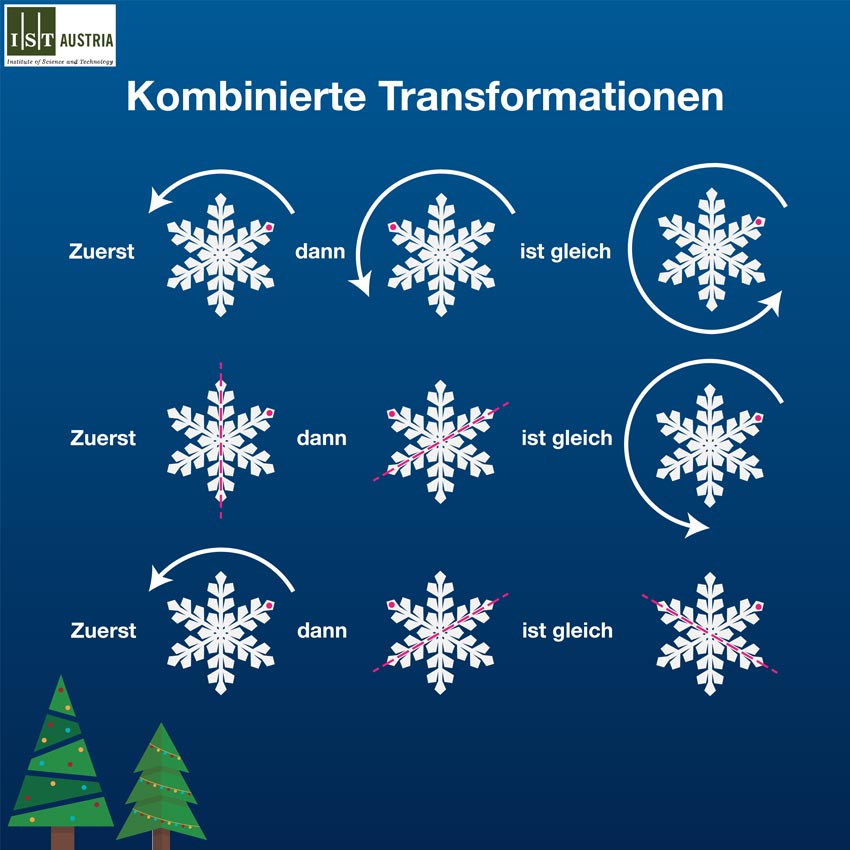
In der Mathematik ist eine Gruppe eine Menge von Dingen mit ganz bestimmten Merkmalen. Im Falle einer Schneeflocke führen die ihr innewohnenden Symmetrien zu einer Reihe von Transformationen mit bestimmten Regeln, wie sie kombiniert werden können, um neue Transformationen zu bilden. Diese Regeln sind es, die eine Gruppe definieren.

Interessanterweise ergibt sich eine eng verwandte Gruppe auch aus den Symmetrien einer Linie mit drei Punkten, die den Ort wechseln können, oder aus der Untersuchung der Lösungen von kubischen Polynomgleichungen. Hier kann man die sonst verborgenen Verbindungen zwischen verschiedenen Bereichen in der Mathematik erkennen. Dies ist ein entscheidender Punkt der Gruppentheorie: Ihr etwas allgemeiner Name deutet darauf hin, dass sie hinter vielen mathematischen Strukturen in unserer Welt steckt.

Buckyballs, Algorithmen und Teilchenphysik

Die Anwendungen der Gruppentheorie sind vielfältig. Die Untersuchung der Symmetrien von Kohlenstoffmolekülen mit Hilfe der Gruppentheorie half beispielsweise bei der Entdeckung des sogenannten Buckyball-Moleküls. Die Wissenschafter:innen, die daran arbeiteten, erhielten dafür 1996 sogar den Nobelpreis. „Ich finde es erstaunlich, dass dieses tiefgehende Konzept einer Symmetriegruppe zur Identifizierung eines Moleküls verwendet wurde“, fügt Tamás Hausel, Mathematiker und Professor am IST Austria, hinzu. Er und seine Kolleg:innen untersuchen viel abstraktere Aspekte von Gruppen, die unterschiedliche Bereiche der Mathematik miteinander verbinden.

In der Informatik ist die Gruppentheorie Teil der mathematischen Werkzeugkiste, die zur Untersuchung von Algorithmen verwendet wird. Sie kann Wissenschafter:innen Aufschluss über die Komplexität einer Berechnung geben und ihnen helfen, Programme zu optimieren, indem sie die Symmetrien des jeweiligen Problems ausnutzen.

In der Physik spielt die Gruppentheorie eine wichtige Rolle in der Quantenmechanik und der Teilchenphysik. Sie gibt den Forscher:innen Aufschluss über die grundlegenden Regeln des Universums. Die Symmetrien der Eigenschaften der Teilchen schreibt vor, wie sie miteinander wechselwirken. Die Wissenschafter:innen stehen jedoch vor dem großen Rätsel, dass sich einige Teilchen anscheinend nicht an die von den Symmetrien vorgegebenen Regeln halten – diese Teilchen brechen die Symmetrie. Darüber hinaus sind sogar die Gesetze der Energie- und Impulserhaltung tief in den Symmetrien unseres Universums verwurzelt, die mit der Gruppentheorie untersucht werden können. All das zeigt, dass uns sogar einfache Dinge wie Schneeflocken dazu bringen können, tief in die mathematische Struktur unserer Welt einzutauchen.